Айлендерс — Тампа-Бэй. Прогноз на НХЛ. 14.01.2019.
Грядущий игровой день Национальной хоккейной лиги подарит нам противостояние между первой и последней командой зоны плей-офф кубка Стэнли восточной конференции. На арене Барклайс Центр Айлендерс примет Тампа-Бэй. Букмекерские конторы считают, что фаворитами встречи являются гости, давайте же разберемся, следует ли брать такой исход во внимание.
Айлендерс
Нью-Йоркский клуб показывает весьма неплохие результаты, правда их не всегда достаточно для того, чтобы занимать хотя бы восьмое место в турнирной таблице восточной конференции. Уже много раз островитяне теряли заветную позиции, однако всегда возвращались. Прошлый тур стал для Айлендерс очень жесткой оплеухой, ведь в дерби Нью-Йорка они проиграли Рейнджерсу, который отстает от них на 9 очков и в рамках нынешнего сезона гораздо слабее сине-оранжево-белых. Такой удар может сильно подкосить команду и начать серию поражений.
В грядущем матче команде не помогут: Ладд и Хики.

Тампа-Бэй
На данный момент, Лайтнинг — лучшая команда Национальной хоккейной лиги нынешнего сезона. Молнии уже набрали 72 очка, ближайший преследователь имеет в своем активе на 13 очков меньше, что является катастрофическим разрывом. Тампа-Бэй вполне спокойно обыгрывает всех своих противников и постепенно продвигается к победе в конференции и взятию президентского кубка.
Следует заметить, что у лидеров чемпионата лазарет пуст.

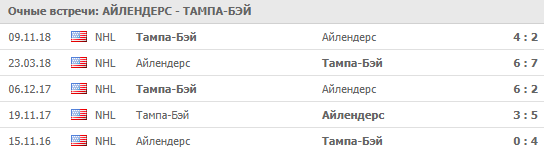
Статистика очных встреч
Интересные факты
- Лайтнинг выиграли 4 из 5 последних встреч;
- Айлендерс выиграли 3 из 5 последних встреч.
Прогноз на противостояние
Мы считаем, что в данном матче победу одержат гости. Отличной ставкой будет чистая победа Тампы с коэффициентом 2,00 по линии 1xstavka.

